POLYNOMIAL

In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. ... Polynomials appear in many areas of mathematics and science.In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. An example of a polynomial of a single indeterminate x is x² − 4x + 7. An example in three variables is x³ + 2xyz² − yz + 1.

Polynomials are sums of terms of the form k⋅xⁿ, where k is any number and n is a positive integer. For example, 3x+2x-5 is a polynomial. Introduction to polynomials. This video covers common terminology like terms, degree, standard form, monomial, binomial and trinomial.

Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry.

The graph of a polynomial function of degree 3

Polynomial functions

A polynomial function is a function that can be defined by evaluating a polynomial. More precisely, a function f of one argument from a given domain is a polynomial function if there exists a polynomial

${\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{2}x^{2}+a_{1}x+a_{0}}$

that evaluates to ${\displaystyle f(x)}$ for all x in the domain of f (here, n is a non-negative integer and a₀, a₁, a₂, ..., a_n are constant coefficients). Generally, unless otherwise specified, polynomial functions have complex coefficients, arguments, and values. In particular, a polynomial, restricted to have real coefficients, defines a function from the complex numbers to the complex numbers. If the domain of this function is also restricted to the reals, the resulting function is a real function that maps reals to reals.

For example, the function f, defined by

${\displaystyle f(x)=x^{3}-x,}$

is a polynomial function of one variable. Polynomial functions of several variables are similarly defined, using polynomials in more than one indeterminate, as in

${\displaystyle f(x,y)=2x^{3}+4x^{2}y+xy^{5}+y^{2}-7.}$

According to the definition of polynomial functions, there may be expressions that obviously are not polynomials but nevertheless define polynomial functions. An example is the expression ${\displaystyle \left({\sqrt {1-x^{2}}}\right)^{2},}$ which takes the same values as the polynomial ${\displaystyle 1-x^{2}}$ on the interval ${\displaystyle [-1,1]}$, and thus both expressions define the same polynomial function on this interval.

Every polynomial function is continuous, smooth, and entire.

Graphs

• 

  Polynomial of degree 0:
  f(x) = 2

 
• 

  Polynomial of degree 1:
  f(x) = 2x + 1

 
• 

  Polynomial of degree 2:
  f(x) = x² − x − 2
  = (x + 1)(x − 2)

 
• 

  Polynomial of degree 3:
  f(x) = x³/4 + 3x²/4 − 3x/2 − 2
  = 1/4 (x + 4)(x + 1)(x − 2)

 
• 

  Polynomial of degree 4:
  f(x) = 1/14 (x + 4)(x + 1)(x − 1)(x − 3)
  + 0.5

 
• 

  Polynomial of degree 5:
  f(x) = 1/20 (x + 4)(x + 2)(x + 1)(x − 1)
  (x − 3) + 2

 
• 

  Polynomial of degree 6:
  f(x) = 1/100 (x⁶ − 2x ⁵ − 26x⁴ + 28x³
  + 145x² − 26x − 80)

 
• 

  Polynomial of degree 7:
  f(x) = (x − 3)(x − 2)(x − 1)(x)(x + 1)(x + 2)
  (x + 3)

A polynomial function in one real variable can be represented by a graph.

• The graph of the zero polynomial
  f(x) = 0
  is the x-axis.
• The graph of a degree 0 polynomial
  f(x) = a₀, where a₀ ≠ 0,
  is a horizontal line with y-intercept a₀
• The graph of a degree 1 polynomial (or linear function)
  f(x) = a₀ + a₁x, where a₁ ≠ 0,
  is an oblique line with y-intercept a₀ and slope a₁.
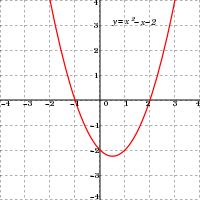
• The graph of a degree 2 polynomial
  f(x) = a₀ + a₁x + a₂x², where a₂ ≠ 0
  is a parabola.
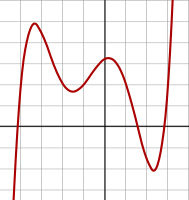
• The graph of a degree 3 polynomial
  f(x) = a₀ + a₁x + a₂x² + a₃x³, where a₃ ≠ 0
  is a cubic curve.
• The graph of any polynomial with degree 2 or greater
  f(x) = a₀ + a₁x + a₂x² + ⋯ + a_nxⁿ, where a_n ≠ 0 and n ≥ 2
  is a continuous non-linear curve.

A non-constant polynomial function tends to infinity when the variable increases indefinitely (in absolute value). If the degree is higher than one, the graph does not have any asymptote. It has two parabolic branches with vertical direction (one branch for positive x and one for negative x).

Polynomial graphs are analyzed in calculus using intercepts, slopes, concavity, and end behavior.